[자료구조] 해시테이블

1. 해시 테이블이란?

 

우리가 누군가에게 연락하기 위해서는 핸드폰 번호를 입력해서 할 수 있겠지만 이런 경우 그 사람의 연락처가 무엇인지 기억하기 위한 노력이 필요합니다. 그런데 만약 100명, 아니 10,000명의 사람의 연락처를 기억하고 그것을 바로 생각해서 연락하는 것은 음, 쉽지 않겠죠?

 

그래서 그것을 기억하기 쉽게 단축 번호(1, 2, ..., N)를 등록하거나 이름, 별명 등 다양한 방식으로 그 전화번호를 저장하는게 보통입니다. 여기서 홍길동이라는 사람의 연락처를 찾는다고 하고, ㄱ~ㅎ까지 순차적으로 확인한다고 하면 등록된 연락처의 수에 비례해서 찾는 시간이 걸립니다.

 

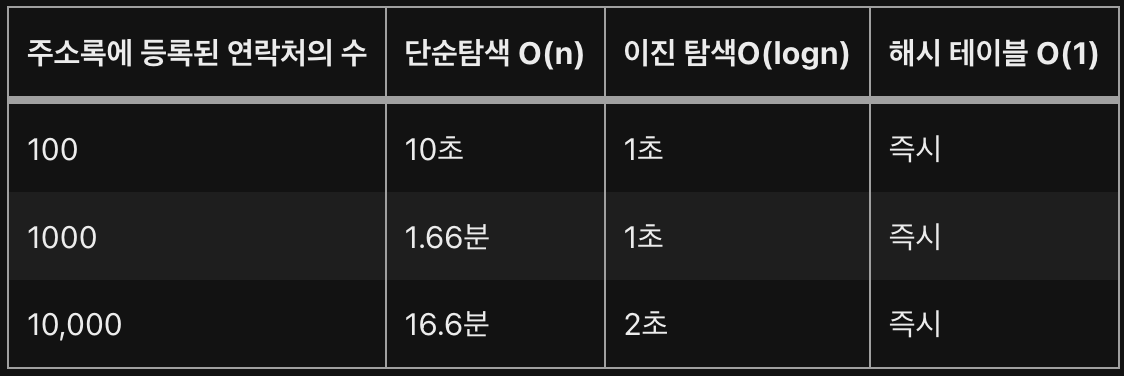
또한 탐색에서 빠르다고 하는 이진 탐색을 이용해도, 탐색하는 양을 절반씩 줄여나가 많이 개선됩니다. 하지만 결국에는 데이터의 양에 절반(logN)만큼 비례해서 찾는 시간이 길어지는 것은 변함 없습니다. 그래서 나온 것이 해시 테이블입니다.

 

해시 테이블은 저장된 자료의 크기에 상관없이 값을 저장하거나 검색하는 것을 할 수 있게 해주는 자료구조 입니다.

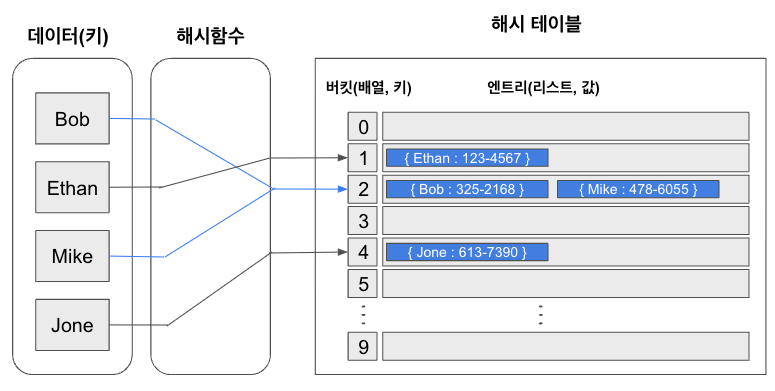
어떻게 해시 테이블은 이렇게 빠른 검색속도가 가능한 것인가 하면 내부적으로 배열을 사용해서 데이터를 저장하기 때문입니다.

 

이 배열에 데이터를 저장하기 위해서는 입력된 값을 Key로 삼아 그것을 해시 함수를 통해 숫자로 반환하고 그것을 배열의 인덱스로 활용해 값을 저장하거나 검색하며 이렇게 값이 저장되는 배열 저장소를 버킷 혹은 슬롯이라고 부릅니다.

 

2. 해시 함수

해시 함수는 문자열을 받아서 숫자를 반환해주는 함수입니다.
어떤 문자열에 대해 숫자를 할당하고 그 숫자가 테이블 안에 키를 보관하고 있는 배열의 인덱스로써 역할을 수행하게 됩니다.

 

데이터에 따라 고르게 분포된 버킷의 인덱스로 배정할 수록 정교한 해시 함수라고 할 수 있으며, 내부에서 이 문자열을 어떻게 숫자로 계산하느냐에 따라 다양한 형태의 해시 테이블이 만들어집니다. 또 매번 값을 저장하거나 검색할 때마다 이 연산 과정을 수행해야하기 때문에 계산이 단순해야합니다.

hash(x) = x mod 13 // 어떤 숫자와 나누냐에 따라 버킷의 범위가 결졍된다. (0~12)

이렇게 해시 함수를 통해 고유한 인덱스를 만드는 것을 해싱이라고 부르며, 대표적으로는 나눗셈을 이용하는 방법, 아스키 코드를 이용한 방법, 곱셈을 이용한 방법, 다수의 해시 함수를 사용하는 방법 등 여러 가지가 있으며 이 방법들을 섞어서 사용할 수도 있습니다.

 

예시로 어떤 문자열을 받았다고 하면 그것을 각 문자에 맞는 아스키코드로 변환할 수 있습니다. 그렇게 그 문자열을 코드로 변환한 숫자의 합을 특정한 숫자와 나머지 연산을 수행해서 나온 값을 해시 값이라고 하며 이를 해시 테이블의 주소(=버킷, 인덱스)로 사용할 수 있습니다.

 

그렇게 주소에 접근하면 그 위치(엔트리)에 값을 저장할 수 있고, 이후 검색을 할 때도 원소의 해시 값을 계산해서 바로 그 위치로 접근할 수 있습니다.

3. 충돌

해시 테이블을 사용할 때 해시 함수가 서로 다른 두 개의 입력 값에 대해 같은 출력을 일으키는 상황을 고려해야합니다.

 

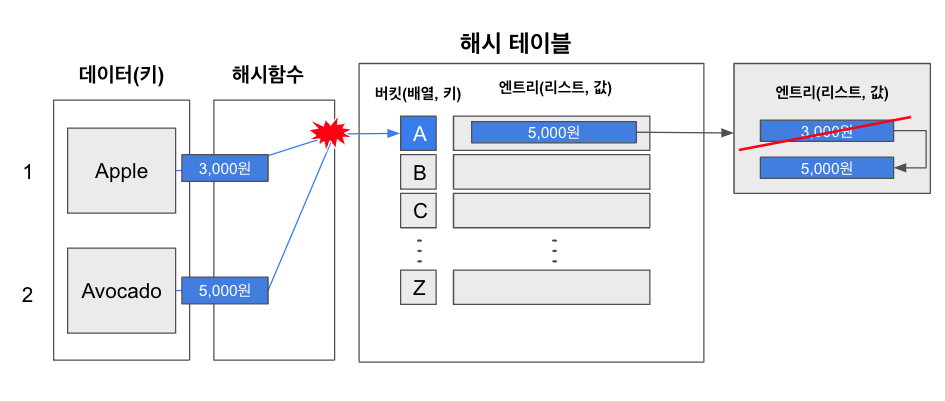
만약 A-Z까지 알파벳을 담을 수 있는 26개의 공간이 있는 배열이 버킷으로 있고 과일에 맞는 가격을 제공하는 해시 테이블을 저장한다고 가정할 때, Apple과 Avocado의 값을 담으려고 하면 해시 함수는 이 입력 값에 대해 동일한 해시 값인 0이라는 인덱스를 반환할 것이고, 이 엔트리에는 2개의 값이 담겨야하는 상황에 놓입니다.

 

이것을 충돌이라고 부르며, 이렇게 충돌이 발생하는 경우 Apple 이후에 들어오는 Avocado에 덮어씌워져 기존에 있던 정보가 지워지고, 나중에 Apple을 조회하면 Avocado의 가격을 확인하게 됩니다.

 

이러한 문제를 해결하거나 개선하는 방법에는 여러 방법이 있으며 크게 분리 연결법과 개방 주소법이 있습니다.

3-1. 분리 연결법(체이닝, Chaining)

 

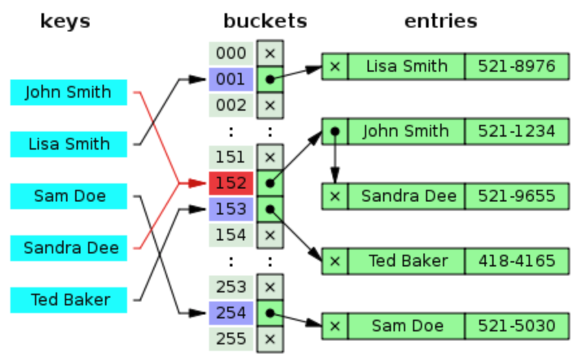
같은 주소로 해싱되는 원소를 모두 하나의 연결 리스트에 담아 관리하는 방법입니다. 원소를 검색할 때 해당 연결 리스트의 원소들을 선형으로 탐색하기 때문에 많은 충돌이 발생하게 된다면 결국 탐색 속도가 O(n)으로 느려진다는 단점이 있습니다.

3-2. 개방 주소법(Open Addressing)

충돌이 일어난 해시 값을 다른 버킷에 삽입하는 방식으로 버킷에 들어갈 인덱스 값을 바꿔 충돌 문제를 해결하는 방법입니다. 그렇기 때문에 원소가 반드시 자신의 해시 값에 일치하는 주소로 저장되지 않습니다.

3-2-1. 선형 조사(Linear Probing)

- 충돌이 일어난 자리(현재 인덱스 위치)에서 고정된 크기만큼 이동하여 차례대로 검색에 비어 있는 버킷에 데이터를 저장합니다.
- 테이블의 최대 길이를 넘어갈 경우 맨 앞으로 돌아갑니다.
- 이 방법 역시 계속해서 빈 자리를 채워갈수록 자리를 찾기 위한 탐색 속도가 증가하여 느려지게 되는 단점이 있습니다.
- 이렇게 공간이 부족한 경우 테이블의 사용률을 계산해서 특정 시점에서 테이블의 공간을 확장하고, 기존의 데이터를 다시 해쉬 함수에 보내서 모든 항목을 다시 재정렬하여 넣는 방식을 취할 수 있습니다.

• 이러한 방식을 리사이징(Resizing)이라고 부르며 사용률 계산은 `해시 테이블의 공간 수 / 해시 테이블에 채워진 항목의 수`를 계산하며 보통 사용률이 0.7을 넘어가면 기존의 크기에 보통 두 배정도의 크기를 만들어서 리사이징 작업을 수행합니다.
• 리사이징을 하면 테이블의 성능도 다시 좋아지고, 충돌도 적게 일어납니다.
• 하지만 이 방법은 많은 시간과 자원을 소모하는 작업 비용이 비싼 방법으로 정말 필요한 상황에 할 수 있도록 잘 고려하여 설계하는 것이 중요합니다.

3-2-2. 이차원 조사(Quadratic Probing)

- 해시의 저장순서 폭을 제곱으로 저장하는 방식으로 충돌의 문제를 해결하는 방법
- 처음 충돌이 발생한 경우 1만큼 이동하고, 그 다음 충돌이 발생하면 2^2, 3^2 칸씩 옮기는 방식을 취합니다.
- 특정 구간에 원소가 몰려있는 경우 그 구간에서 빨리 벗어날 수 있는 장점이 있습니다.
- 최초 해시 값이 같은 경우 이전에 충돌하면서 빈 버킷을 탐색했던 루트를 그대로 따라야 하는 단점이 있습니다.

• 28 : 2 -> 3
• 41 : 2 -> 3 -> 6
• 67 : 2 -> 3 -> 6 -> 11

3-3-3. 더블 해싱(Double Hashing)

- 해시된 값을 한 번 더 해싱하여 해시의 규칙성을 없애면서 충돌의 문제를 해결하는 방법
- 한 해시 함수는 최초의 해시 값을 얻을 때 사용하고, 다른 해시 함수는 충돌에 대한 이동 폭을 얻을 때 사용합니다.
- 해싱하는 연산을 두 번 수행하는 만큼 다른 방법들에 비해 많은 연산을 수행하는 단점이 있습니다.

4. 성능

해시 테이블은 같은 입력 값에 대해서 항상 같은 출력 값이 보장되어야 하고, 서로 다른 입력 값으로부터 동일한 출력 값이 나올 가능성이 적어 무결성을 보장합니다. 평균적으로 모든 항목에 대해 O(1) 시간이 소요되며, 데이터의 크기에 영향을 받지 않습니다.

평균적인 경우 해시테이블의 성능은 탐색에서는 배열만큼 빠르고, 삽입과 삭제는 연결 리스트만큼 빨라 양쪽의 장점을 모두 가지지만 최악의 경우를 가정할 때는 해시 테이블이 가장 안좋은 성능을 보이기도 합니다.

 

그렇기 때문에 해시 테이블에는 최악의 상황이 발생되지 않도록 하는 것이 중요하고, 그렇게 하기 위해서는 이 충돌 문제를 해결해야 합니다.

5. 해시의 응용

1) SHA(Secure Hash Alogirhtm)

• 보안 해시 알고리즘이라고 부르며 1993년 NSA에 의해 개발된 해시 알고리즘입니다.
• SHA-0, SHA-1 함수 군은 해시 충돌성이 있어 취약점이 존재하며 현재 주로 사용되는 것은 SHA-2 함수 군으로 다이제스트의 길이에 따라 SHA-256, SHA-512 등으로 나뉩니다.
• 일방향으로 문자열에서 해시 값을 얻을 수는 있지만 그 반대의 경우는 불가능합니다.
• 파일을 비교하거나 패스워드 확인하는 목적으로 사용합니다.

2) 무결성 검사(전사 서명 등)

3) 블록체인
4) 데이터베이스에 비밀번호 저장
5) Git Commit
6) 캐싱(Caching)